From the Markowitz model to EasySampling optimization: evolved tools for modern financial advice
Correlation is like a silent dance between assets: some move in unison, others repel, and still others seem to ignore each other. But what happens when this dance changes pace, in a financial world where the unexpected is the only constant? In this scenario, relying on a static snapshot of the past is no longer enough. A dynamic model is needed, a more conscious eye: robustness is needed.
The correlation matrix: theoretical foundation and structural limitations
The correlation matrix is one of the cornerstones in portfolio theory. It encodes, with mathematical rigor, the linear interrelationships between the returns of financial instruments. In a square, semi-positive matrix[1] each element represents a Pearson correlation coefficient between two assets, measuring their synchrony or disagreement in price movements.
In the context of Modern Portfolio Theory, the matrix becomes the main tool for minimizing the overall portfolio variance, enabling the construction of the so-called efficient frontier. However, this theoretical elegance often breaks down with the instability of real markets. The 2008 financial crisis, the collapse of technology stocks in 2000, or even the COVID-19 pandemic have shown how historical correlations can crumble very quickly, leaving portfolios exposed to systemic risks not predicted by the theoretical model.
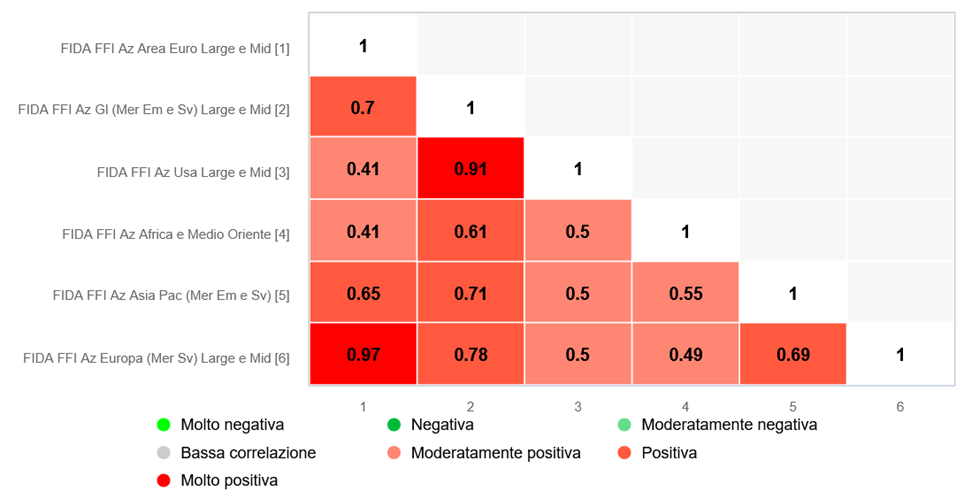
Source: FIDAworkstation
The illusion of stability
Classical models assume that correlations and variances are stable over time and perfectly estimable. But the reality is quite different: macroeconomic shocks, exogenous events and regime transitions[2] make correlations highly unstable. Point estimates therefore risk producing portfolios that are optically optimal but practically dysfunctional, with over-concentration and inconsistent performance.
This problem worsens as portfolio size increases: the more securities one includes, the more difficult the correlation matrix becomes to estimate correctly, with the risk of introducing noise rather than information. In addition, aggregate investor behavior can cause so-called “panic correlation,” in which traditionally decorrelated assets move in unison at times of crisis, thwarting the illusion of diversification.
The robustness paradigm: beyond photography, toward film
Robust optimization was created in response to this critical issue. Instead of relying on a single correlation matrix, it considers the uncertainty inherent in the parameters. The result is a portfolio that is less sensitive to estimation error and more stable as scenarios change.
Some robust approaches introduce confidence intervals on the estimated parameters, assuming that these are not fixed but distributed within a range of statistical plausibility. In this view, the optimal portfolio is no longer the one that maximizes the expected return on a single scenario, but the one that maintains its properties over a family of alternative scenarios.
Bayesian methods, for their part, supplement point estimates with a priori information: instead of treating parameters as certain values, they treat them as random variables with probability distributions. This allows the incorporation of expert knowledge, external data or market insights, making the final allocation a compromise between historical evidence and analytical judgment.
Finally, bootstrap simulations are an extremely effective nonparametric technique for testing the resilience of portfolios. Through re-sampling with reinsertion of historical observations, they generate a multitude of alternative scenarios that retain the starting statistical characteristics but explore the full spectrum of possible evolutions. The portfolio that proves robust across multiple simulations is more likely to perform consistently in the real world as well.
The concept of robustness is not synonymous with conservatism, but with an awareness of data imperfection. Building a robust portfolio means embracing uncertainty, not evading it; it means designing for variability, rather than hoping for stability.
EasySampling with FIDAworkstation
This is where EasySampling, the mean-variance optimization module built into the FIDAworkstation platform, comes in. The method consists of sampling the historical horizon into ten annual sub-periods, representative of different scenarios. Correlations, variances and returns are calculated for each sample, constructing ten different efficient frontiers.
The methodology ideally follows the statistical bootstrap: by dividing the time frame into independent sub-periods, a polychromatic view of the investable universe is obtained, reflecting a multiplicity of market conditions, from bull to recessionary regimes.
The use of the FIDA FFI (FIDA Fund Index) database ensures broad cross-asset coverage, based on quality-certified data. The choice of annual samples over a 10-year horizon allows for capturing cyclical variations and stressing the portfolio against heterogeneous conditions.
The end result is an average asset allocation: more robust, less affected by abnormal events, and able to reflect the dynamic and imperfect nature of markets. The output can be fully integrated into the financial advisor’s operational flow, thanks in part to the graphical and comparative features offered by the platform.
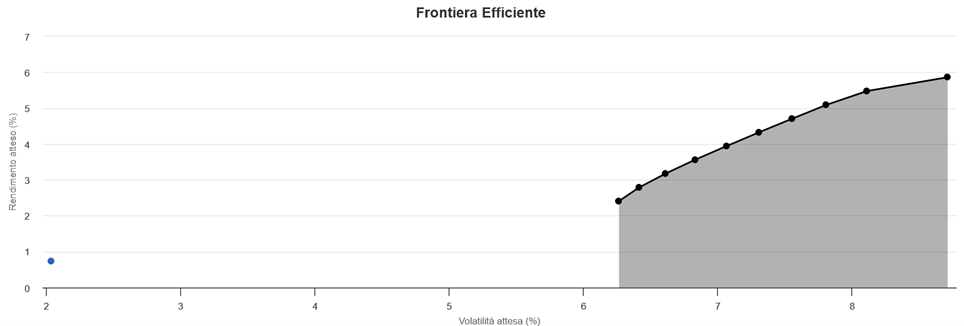
Source: FIDAworkstation
A more human approach to management: antifragility applied to portfolios
Far from being a technical quirk, robustness is a different way of thinking about advice: no longer as an art of prediction, but as an architecture of resilience. EasySampling enables the professional to build portfolios that not only resist change, but benefit from it.
The reference to the Taliban concept of “antifragility” is not accidental: a portfolio built on asset allocations mediated by different historical regimes tends not to collapse in the presence of stress, but rather to take advantage of momentary market inefficiencies. Thus, it is not just about defending capital, but thriving in disorder.
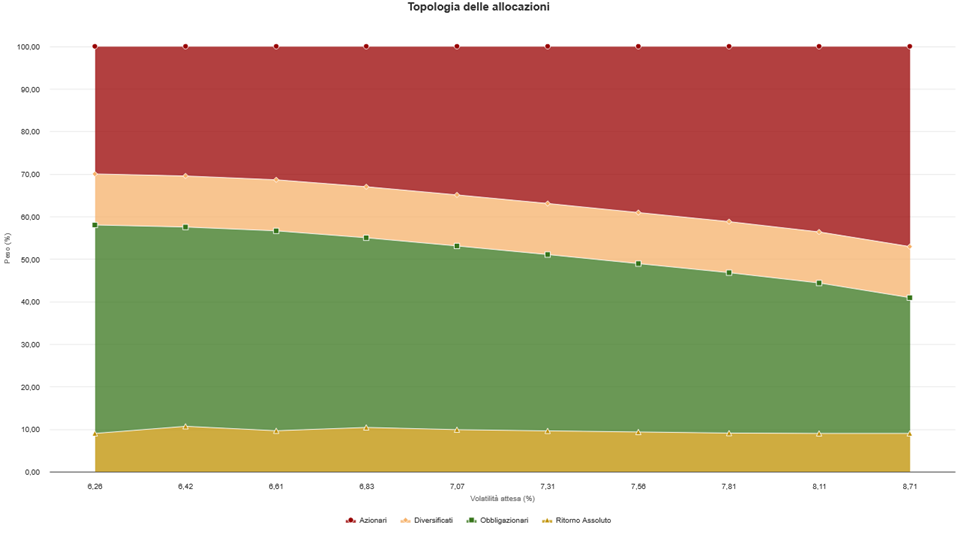
Source: FIDAworkstation
Advisory as uncertainty engineering
In the transition from theory to practice, the correlation matrix loses its guise as a perfect tool to become a critical object, to be handled with awareness. Advanced modules such as EasySampling represent the natural evolution of a mature approach: one that knows that uncertainty is inevitable, but not unmanageable.
Coupling portfolio theory with sophisticated but intuitive computational tools does not mean betraying its mathematical elegance, but rather translating it into operational efficiency. In this sense, FIDAworkstation stands as a valuable ally of the contemporary advisor: not as an oracle, but as a rational workshop in which quantitative analysis becomes an everyday craft.
References:
- Markowitz, H. (1952). Portfolio Selection. Journal of Finance.
- Efron, B. (1979). Bootstrap Methods: Another Look at the Jackknife. Annals of Statistics.
- Ben-Tal, A., & Nemirovski, A. (2002). Robust Optimization – Methodology and Applications. Mathematical Programming.
- Meucci, A. (2005). Risk and Asset Allocation. Springer
- Elton, E. J., Gruber, M. J., Brown, S. J., & Goetzmann, W. N. (2014). Modern Portfolio Theory and Investment Analysis. Wiley
- Taleb, N. N. (2012). Antifragile: Things That Gain from Disorder. Random House.
Monica F. Zerbinati
![]()
Request a free trial at welcometeam@fidaonline.com
Full article at www.we-wealth.com