Valutare il rischio di un andamento inatteso dei rendimenti di un investimento è uno dei compiti più complessi di un’analista. I fattori che possono influenzarne l’andamento sono molteplici, e spesso molto difficili da prevedere. Trovare una giusta misura della volatilità, o variabilità dei rendimenti, diventa quindi fondamentale.
La soluzione più comunemente adottata è l’utilizzo di un indice statistico, la deviazione standard o scarto quadratico medio. Questo indicatore misura lo scarto che mediamente le singole osservazioni dei rendimenti hanno rispetto alla loro media, misurando quindi il grado di dispersione dei rendimenti. Più esso è alto, più il rischio che i rendimenti si discostino da quelli desiderati o attesi sarà elevato.
Il calcolo di questo indicatore è semplice e intuitivo. Prendendo un campione sufficientemente grande di rendimenti xi con i = 0,1, … , N e N numero di osservazioni nell’orizzonte temporale considerato, la deviazione standard dei rendimenti σX può essere definita come segue:
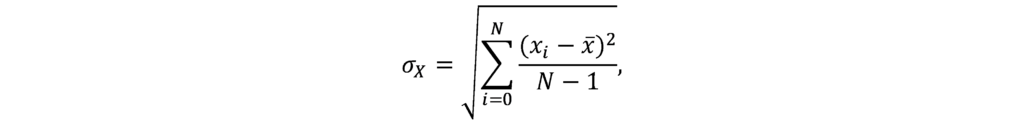
con:
- N numero di osservazioni dei rendimenti;
- xi rendimento dell’asset nel periodo i-esimo;
- x_ rendimento medio nel periodo considerato.
Il campione di rendimenti considerato, come è naturale, si riferisce necessariamente ad un periodo antecedente ad oggi, sufficientemente lungo e che noi consideriamo indicativo dell’andamento futuro del titolo.
Il valore che otteniamo attraverso questa formula misura gli scostamenti dalla media sia in negativo che in positivo, non facendo distinzioni tra le performance positive e negative del titolo all’interno del calcolo. Questo però non considera il comportamento effettivo di un investitore: in un’ottica di investimento quando si considera il rischio di cambiamenti inattesi nel valore di un asset generalmente l’obbiettivo è quantificare le possibili perdite, favorendo invece la possibilità di scostamenti positivi nei rendimenti.
È necessario quindi trovare un metodo per misurare il cosiddetto downside risk, cioè il rischio che vi siano rendimenti inferiori a quello atteso o, più correttamente, a quello desiderato dall’investitore. La più classica misura di downside risk è sicuramente la semivarianza, che ha una formula molto simile alla varianza ma con alcune differenze. Utilizzando lo stesso campione di rendimenti xi come nel caso della deviazione standard, possiamo definire la semivarianza SVX come:
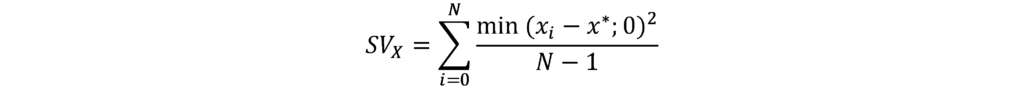
con:
- N numero di osservazioni dei rendimenti;
- xi rendimento dell’asset nel periodo i-esimo;
- x* rendimento target dell’investitore.
La funzione min() al numeratore indica che verrà preso il valore minore tra la differenza tra i rendimenti dell’asset e il rendimento target e 0. L’utilizzo di questa formula permette infatti di considerare nel calcolo solamente quei rendimenti che sono inferiori al livello di performance target dell’investitore. Il rendimento target può essere la stessa media dei rendimenti oppure un’altra grandezza definita a priori: una scelta comune è l’utilizzo di un tasso risk free, che può essere considerato sia costante nel tempo sia variabile periodo per periodo.
Estraendo la radice quadrata della semivarianza otteniamo un indice del tutto simile alla deviazione standard, ma che considera esclusivamente le perdite. Questo valore indica l’entità media di quest’ultime, dando una misura più centrata sui rendimenti negativi.
La semivarianza non è l’unica misura di rischio che si concentra sulle perdite: anche altre misure più sofisticate, come il Value at Risk e l’Expected Shortfall, concentrano l’attenzione su di esse. Le due misure che abbiamo trattato, però, sono sicuramente le più utilizzate per la loro semplicità ed applicabilità, e rappresentano la base delle più comuni teorie di ottimizzazione del portafoglio.
Trovi tutti gli approfondimenti su questo argomento qui.
Ulteriori approfondimenti su Enciclopedia della Finanza.




